DOI: 10.24308/iass-2014-150

LUISS University, Roma, Italy

procchi@luiss.it

Abstract

Semiotics provides fundamental contributions to illuminate the present ‘information revolution’, however a certain distance seems to separate semioticians from the experts of digital technology. In the past centuries, cultural divisions occurred between philosophers and experimentalists in other scientific fields too, and later their positions got closer. This paper holds that also the stances of semioticians and electronic engineers could approximate. They could meet in a terrain of study – herein denoted as ‘mathematical semiotics’ – that translates basic semiotic concepts into the mathematical language. In turn the mathematical expressions can clarify some misconceptions and false impressions. As a case study, we shall define the notion of signifier in formal terms and show how this definition spells out some aspects of the digital and analog technologies, and can answer to some philosophical issues.

1. A special divide

Let us begin with a pair of remarks.

In 1897 Joseph John Thompson discovered the electron, and inaugurated a period in which there was considerable speculation about the atomic particles existing in nature (Yang 1963). Nearly a decade later Ernest Rutherford performed a fundamental experiment to test the inner structure of the matter. This evidence and other finding led scientists toward the complete understanding of the atom which includes three fundamental particles: electrons, protons andneutrons. All those researches – backed up by abundant equations and calculations – opened the way to modern atomic physics and to the atomic energy appliances created for military and civil purposes (Cantelon, Hewlett and Williams 1992), (Lavine 2013).

Semioticians discovered the ‘atomic’ parts of signs. They became persuaded that a sign is equipped with three basic elements: the signifier, the signified and the referent (Morris 1938),(Thibault 1996). Richards and Ogden (1989) formalized them into the semantic triangle, however semiotics did not usher in the digital revolution.

The ‘atomic age’ stemmed from the studies of physicists who are still driving this event. By contrast, semioticians did not play a leading role in the launch of the ‘information age’ even though semiotic notions lie at the heart of electronic equipment. Why this difference?

As second, we observe that digital images, sound, film movies and other forms of data can be stored by any number of methods: magnetically, optically, electronically or even otherwise (Wang and Taratorin 1999). Cathode-ray tube, liquid crystal display, light {XE “light”} -emitting diode {XE “LED”}, touch screen and gas plasma exhibit ever better images (Castellano 1992) {XE “images”}. Researchers look into the physical properties of signs such as Leo Szilard who envisioned a theoretical engine to seek out the minimal sign available in nature (Devereux 2003). Quantum physicists calculate the information conveyed by atomic particles. We mention this variety of studies just to say that the researches on {XE “technology”} signifiers are progressing in the information and communication technology (ICT) and are so successful as they transform the lifestyles of people worldwide.

Scientists coming from various fields work on semiotic elements all the day long, but are not inclined to quote semiotic literature. The doers of digital systems rarely study semiotics and utilize the semiotic notions in a rather intuitive way. Why does semiotics, which establishes fundamental tenets, is felt as a foreign discipline by ICT experts?

It is not necessary to make a special inquiry to put forward an answer to the previous two queries. As long as one examines the work-styles of semioticians and technicians, he can note some blatant differences between the two groups. The latter focuses on the material properties of signs that describes in terms of numbers. Engineers adopt graphs, diagrams, and the mathematical language to calculate machines and products. By contrast, the former group does not employ mathematical expressions even when it examines the material side of communication. Great semioticians – e.g. Whitehead, Wittgenstein and Peirce (1992) – had strong background in logic, mathematics, and science, but prefer to look into the full complexity of language rather than into technical applications. Semioticians concern themselves with the interpretation of signs in accordance with the human knowledge. They investigate global phenomena originated from the mind in all aspects.

Semioticians use verbal descriptions. Engineers use formal expressions. Nowadays a specialdigital divide which is essentially a cultural divide separates semioticians and engineers.

2. History repeats itself

In the past, thinkers and technicians often worked about the same area following distinct directions. The two groups eventually found out consensus of opinions and succeeded in cooperating. For instance, the idea that matter is composed of discrete units and cannot be divided into arbitrarily tiny quantities emerged early since the 5^th century BC with Leucippus, whose student, Democritus, systematized his views (Pullman 1998). In particular Democritus coined the term ‘άτομος (atom)’ and in the 19^th century the scientists who detected the elementary components of the matter retained the term ‘atom’ coined by Democritus to underline the continuity extant between ancient thinkers and modern experimentalists.

In 1687, Isaac Newton published “Philosophiæ Naturalis, Principia Mathematica” a book which states the foundation of classical mechanics. This title means to say that the mathematical principles – principia mathematica in Latin – state broad topics pertaining to the philosophy of Nature – philosophiæ naturalis in Latin. In an indirect manner, Newton recognizes how philosophers and mathematicians have acted together down throughout the centuries. They worked toward a common goal. Historicians assign major authors such as Aristotle, Galileo and Lagrange to this broad movement, and minor thinkers such as Sébastien Basson whose work ([1621] 2009) has been recently republished.

It is our opinion that something like should be established in the present information society. A bridge should connect humanities and engineering. The semiotic notions – especially the formal definition of the signifier that technicians manipulate all the day long – should be translated into the mathematical language. That is why we are inclined to call this bridge mathematical semiotics.

3. Analyticity & mathematics

Factually modern technicians concentrate on tiny components including electric impulses, dots of ink, pixels (picture elements) in the display screen, infinitesimal pits on the surface of a compact disk, holes in the computer cards and so forth (Pohlmann 1992)(Saffady 1990). The astonishing performances of electronic systems are based on the physical properties of Lilliputian components which seem trivial elements to a humanist. As electrons, neutrons and protons ensure the enormous power of an atomic power unit, in a similar manner microscopic signifiers ensure the astonishing performances of electronic appliances and play essential roles in ICT. As an example, figure 1 exhibits four signifiers devised at different times that provided evident benefits to a large number of users.

Fig. 1: The digit 8 with the Morse code a), the bar code b), American standard code for information interchange (ASCII) c) and the seven-segment code d).

Technicians reject philosophical systems in favour of attention to details. They tackle practical problems one at a time, instead of having to invent at one stroke a block theory of the whole universe. They follow an anlytical method of study which is appropriate to the mathematical language. It may be said that analiticity implies mathematics and vice versa.

3. Elementary signifiers

The so called mathematical semiotics can but share the analytical approach typical of engineering and we can but begin with looking into the tyniest signifiers.

An elementary signifier or sense datum can be analyzed at ease because it does not have any structure or pattern. An elementary signifier comes to life by means of a detecting action. Detection consists in perceiving a physical value and does not require any recognition, realization or interpretation.

An elementary signifier is perceived by a small artificial probe, a simple biological receptor, a sensor or something like which we call ‘referent’ or ‘observer’ R. Experimental observations demonstrate that the necessary requisite for R to sense the elementary signifier E is that E is clear respect to the signifier E* that may be the background, the context or any close entity. One can even establish a scale to measure the quality of being distinct for E. When E contrast with E*, E is a perfect signifier. If E and E* partially overlap, than E is low quality. Finally, if E is completely confusing, it disappears and in consequence there is no sign. Factually a sign does not exist and does not carry on any meaning when the physical base E is not distinguishable.

Universal experience shows how sharpness is the fundamental character of signifiers, and in turn of signs. This physical property waits to be translated into a mathematical expression and we put forward the following way (Rocchi and Gianfagna 2006).

We tell that the object E is a signifier if E is not equal (literally with the symbol ‘NOT=’) to the adjacent entity E* with respect to the observer R

E NOT=R E*                                (1)

This statement entails that whenever (1) is true, the object E is a sign. If the inequality (1) is false, E remains an object without any semiotic property.

The inequality (1) could be called the principle of sharpness and ferries the semiotic notion of signifier to the engineering domain.

Engineers do not recognize (1) in formal terms but apply (1) in the communication and information technology on a somewhat intuitive basis. Technicians recognize that signals are to be sharp using an empirical criterion. Let us examine a noteworthy case.

Circuits exchange electric values which are elementary signifiers. In fact, engineers use the high-level voltage V1 and the low-level voltage V2 – called bits – which are distant. Technicians describe electronic bits using this equation (Plant 1990)

V1  ≠ V2                                        (2)

The symbols ‘≠’ is equivalent to ‘NOT=’. Bits conform to inequality (2) that is identical to (1) with the difference that (1) has general meaning, instead (2) regards only electrical voltage values. The inequality (2) clarify that digital technicians employ discrete elements because discrete elements turn out to be distinct one from the other and ensure the appliances to run effectively. Engineers pay great attention to the separation s of bits that they derive from the inequality (2)

s = | V1 – V2 | ≠ 0                          (3)

Factually, environmental disturbance and interference intrinsic to the electrical circuits affect the bits. The voltage values vary during the time and the signifiers V1 and V2 risk to overlap and to become confusing. The difference between ideal bits and real bits appears in figure 2 and 3.

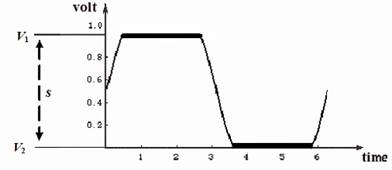
Fig. 2: Ideal form of bits.

Minor disturbances bring V1 and V2 nearer and engineers determine the separation s so adequately that the digital signifiers remain distinguishable due to a residual distance. Even if the high-value V1 and the low-value V2 fluctuate, the bits continue to be distinct because of the prudently chosen size of s.

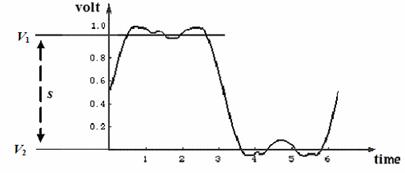
Fig. 3: Minor distortion of bits.

Obviously the larger is the separation s and the higher are the energies spent for capturing, recording, processing, storing, and transmitting signals. Engineers tune up (3) with respect to effectiveness of appliances. They balance s against insulation, power supply and other involved electrical parameters.

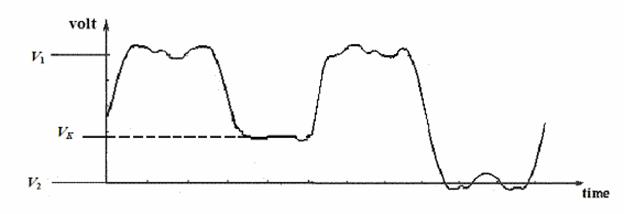
Fig. 4: Major distortion of bits.

The prudent size of s cannot impede that major electrical disturbance upset the rule (3). Heavy interference results in a new voltage value that occurs in the place of regular bits. For example the wrong value VK appears in figure 4.

Engineers are aware of this type of situations. They guarantee the stability {XE “stability”} of the binary alphabet in that electronic appliances do not accept an altered value but associate it to the bit V1 or otherwise to the bit V2. The receiver handles regular bits anyway.

4. The philosophical side of a mathematical expression

Semioticians tend to overlook the efforts made by engineers to set up bits and to make bits running under the worst situations. Humanists are not inclined to go deep into the technology and thus they discuss ICT from a view point which may be defined as ‘external’ to technology. Theyobserve devices from the outside. For example, several commentators conclude that the digital offers representations rather unnatural while the analog signals are more natural and closer to something that happens elsewhere (Blachowicz 1998).

The mathematical study of semiotics conducted in the previous section demonstrates the contrary is true.

Digital signals are absolutely neat. It may be said that bits are authentic signifiers which comply with the principle of sharpness even under challenging situations. Instead, analog signals are frequently imprecise and fuzzy, they cannot be classified as reliable elements.

Bits are able to represent whatsoever object, entity, or text. Digital signs are flexible in semiotic terms; hence one should conclude that they are very good signifiers and conform to the principle of arbitrariness by Saussure ([1916] 1983). The analog does not convey intentional or symbolic meanings in the so easy manner as the digital can do. Frequently the sense of the analog signal is obligatory, in that significance is motivated by the physical aspect of the signal. For instance growing electrical values cannot represent a decreasing physical event.

Discrete signals provide faithful reproductions even in terms of realism. The digital camera stores a sequence of bits in an electronic chip and then a computer printer provides the final image – consisting of discrete elements – which appears identical to the portrayed original. A high-quality digital image – say an image including over 2000 dpi (= dots per inch) on paper – appears absolutely realistic and no one would be able to distinguish between the computer print and the traditional analog print. Discretization demonstrates to be in keeping with the reality in the most perfect way (Rocchi 2012).

In conclusion, discrete signals offer accurate reproductions of sound, images, film movies etc. The digital turns out to be more natural than the analogue in the sense that digital signs comply with basic laws which are the sharpness and the arbitrariness principles.

The principle of sharpness tells that the object E is a good signifier when it shows blatant dissimilarities with E*. The object E is a lower-quality signifier when differences diminish. Finally the sign E does not exist if it coincides with E*, or it is fuzzy or anyway it is not distinct. The principle (1) sustains the material aspect of signs moreover it provides novel cues on vexed philosophical arguments about the physicism of signs.

Some authors put forward some paradoxes to disprove the physical nature of signs. For example Wiener (1961) raises this conundrum:

· When people always get the same signal, why this becomes inessential and nothing may be transmitted with the same result?

Others who deny the material base of signs pose the following queries:

· Nothing (that is to say an empty space or a silence) convey meaning; how can one assert that signifiers are concrete if signs are bodiless?

· A sign is extant provided that it is perceived and no longer exists if nobody detects it; if a sign has a material origin, how can it come to life and perish?

The discussion of the previous philosophical arguments goes beyond the scopes of the present work. However it may be showed how the inequality (1) can provide innovative answers to the above listed question points (Rocchi 2012).

In sum, the mathematical language does not confine us to handle minute elements which provoke negligible consequences. Instead the calculus of tiny digital signifiers accelerates the pace of mankind progress, and also aids thinkers to tackle broad philosophical arguments.

5. Conclusion

This paper means to stimulate a discussion on the cultural gap extant between semioticians and ICT experts. One can learn from the history of science how this gulf is not impossible to fill provided that both the circles of scholars advance toward each other. We believe that humanists and engineers could meet in the mathematical study of semiotics whose introductory traits have been summarized. The previous pages demonstrate how this cultural encounter could come into effect.

Presently, ICT experts adopt empirical approach, and resort to occasional ideas. Instead they could obtain solid principles for digital systems on the condition that they study semiotics in deep. They could improve the methods of work and could clarify a series of issues. On the other hand, humanists could discover the substantial impact of some technical factors that they deem negligible so far. Even philosophers could benefit from the mathematical description of semiotic concepts that suggest innovative cues.

In summary, the mathematical definitions of semiotics could provide an exhaustive theoretical base to digital technologies, and semioticians could become able to play more significant role in the present information age, which is technology based.

References

BASSON, S. [1621] 2009. Philosophiae naturalis adversus aristotelem. Libri XII. Lamarra A., Palaia R. (eds.), Lessico Intellettuale Europeo, vol. 106, Leo S. Olschki Editore, Firenze.

BLACHOWICZ, J. 1998. Of two minds: The nature of inquiry. Suny Press, Albany.

CANTELON, P.L., R.G. HEWLETT & R.C. WILLIAMS. 1992. The american atom: Documentary history of nuclear policies from the discovery of fission to the present. University of Pennsylvania Press, Philadelphia.

CASTELLANO, J.A. 1992. Handbook of display technology. Academic Press, San Diego.

DE SAUSSURE, F. [1916] 1983. Course in general linguistics. Duckworth, London.

DEVEREUX, M. 2003. A modified szilard engine: Measurement, information, and maxwell's demon. Foundations of Physics Letters, 16(1). 41-55.

LAVINE, M. 2013. The first atomic age: scientists, radiations, and the american public, 1895–1945. Palgrave Macmillan, Basingstoke.

MORRIS, C.W. 1938. Foundations of theory of signs. University of Chicago Press, Chicago

OGDEN, C.K. & I.A. RICHARDS. [1923] 1989. The meaning of meaning. Harvest/ HBJ, San Diego.

PEIRCE, C.S. 1992, 1998. The essential Peirce: Selected philosophical writings. Houser N., Kloesel C.J.W. (eds.), vol. 1 &2, Indiana University Press, Bloomington.

PLANT, M. 1990. Basic electronics. Hodder Education, London; 2nd Revised edition.

POHLMANN, K.C. 1992. The compact disc handbook. Oxford University Press, Oxford

PULLMAN, B. 1998. The atom in the history of human thought. Oxford University Press, Oxford.

ROCCHI, P. 2012. Logic of analog and digital machines. Nova Science Publishers, N.Y.; 2nd revised edition.

ROCCHI, P., Gianfagna L. 2006. An introduction to the problem of the existence of classical and quantum information. AIP Conference Proceedings, 810(1). 248–252.

SAFFADY, W. 1990. Optical discs versus magnetic storage. Information Today, Medford, NJ

THIBAULT, P.J. 1996. Re-reading Saussure: The dynamics of signs in social life. Routledge, London.

WANG, S.X., Taratorin A.M. 1999. Magnetic information storage technology. Academic Press, San Diego.

WIENER, N. 1961. Cybernetics or the control and communication in the animal and the machine. MIT Press, Cambridge; 2nd edition.

YANG, C.N. 1963. Elementary particles: A short history of some discoveries in atomic physics.Princeton University Press, Princeton.